STAT 479 Lecture 10

NFL WAR

Recap: EPA in Football

• 86-yard touchdown by Ladd McConckey on a pass from Justin Herbert (video link)
  • Thrown on a 3rd and 26 from Chargers’ 14 yard line. EP = -1.54
  • Chargers generated 7 - (-1.54) = 8.54 points of EP
• 64-yard touch down by Kavontae Turpin on a pass from Cooper Rush (video link)
  • Thrown on 3rd and 10 from Cowboys’ 36 yard line. EP = 0.77
  • Cowboys generated 7 - 0.77 = 6.23 points of EP

• How should we divide credit between QB and receiver?
• What about running?

Plan

• Estimate EPA per-play for each passer, receiver, & rusher
• Separately model three phases:
  • Passing I: EPA due to actions while ball is in the air
  • Passing II: EPA due to yards after catch
  • Rushing
• Multi-level modeling:
  • Random intercepts for passers, receivers, rushers
  • Must adjust for important fixed effects

• W/ per-play EPA can compare actual production to replacement “shadow”
• These contrasts will lead to a version of WAR

Data Preparation

Overview

• Focus on 2024-25 regular season
• Need roster data to define position-specific replacement level

Passing Data

• Extract all passing plays (play_type == "pass")
• For each pass, record
  • posteam, defteam, posteamtype
  • passer_player_id, receiver_player_id
  • shotgun, no_huddle, qb_hit, pass_location
  • air_yards, yards_after_catch, completed_pass

table(pass2024$pass_location)

  left middle  right 
  6373   3810   6817 

Air vs YAC EPA

• Teams generate EPA on completed passes while
  • The ball is in the air
  • On the ground, after the catch
• nflfastR decomposes epa into air_epa and yac_epa
• Completed passes: imagine pausing game as soon as catch completed
  • EP at the intermediate state used to compute air_epa and yac_epa
• Sacks: no good definition for air_epa & yac_epa
  • We will treat sacks as rushing plays

Rushing Data

• Include columns for
  • passer_player_id & rusher_player_id
  • shotgun & no_huddle
  • run_location & run_gap
• Must manually specify rusher_player_id on sacks

Run Context I

• run_location indicates direction

  left middle  right 
  5425   3565   5172 

• run_gap:
  • "guard": runs through B gap (b/w guard & tackles)
  • "tackle": run through C gap (outside tackle or b/w tackle & end)
  • "end": run through D gap (outside TE)
  • NA: run through A gap (b/w center & guard)

        run_location
run_gap  left middle right <NA>
  end    1958      0  1805    0
  guard  1822      0  1739    0
  tackle 1645      0  1628    0
  <NA>      0   3565     0 1447

Run Context II

• We will create a new variable run_context
• Concatenate run_location & run_gap when both not NA
• For “A” gap runs, run_context = "middle"
• For sacks & fumbles, set run_context = "other"
• Additionally add posteam: proxy for offensive linemen & blockers

rush2024 <-
  rush2024 |>
  dplyr::mutate(
    run_context = dplyr::case_when(
      run_location == "middle" ~ paste(posteam, "middle", sep = "_"),
      is.na(run_location) & is.na(run_gap) ~ paste(posteam, "other", sep = "_"),
      .default = paste(posteam, run_gap, run_location, sep = "_")))

Team Strengths

• Important to account for teammates & opponent quality (recall Lecture 4)
  • Don’t overly reward players on good teams
  • Don’t overly penalize players on bad teams
• Measure passing & rushing strength with mean EPA
• Add columns to pass2024 and rush2024

pass_strength <-
  pass2024 |>
  dplyr::group_by(posteam) |>
  dplyr::summarise(pass_strength = mean(epa,na.rm = TRUE))
rush_strength <-
  rush2024 |>
  dplyr::group_by(posteam) |>
  dplyr::summarise(rush_strength = mean(epa, na.rm = TRUE))

pass2024 <-
  pass2024 |>
  dplyr::inner_join(pass_strength, by = "posteam") |>
  dplyr::inner_join(rush_strength, by = "posteam")

rush2024 <-
  rush2024 |>
  dplyr::inner_join(pass_strength, by = "posteam") |>
  dplyr::inner_join(rush_strength, by = "posteam")

Modeling Passing EPA

Composite Outcomes

• \(\Delta\): observed EPA on a passing play
• \(\delta_{\textrm{air}}\) and \(\delta_{\textrm{yac}}\): air_epa and yac_epa given by nflfastR
• Decompose \(\Delta = \Delta_{\textrm{air}} + \Delta_{\textrm{yac}}\) where \[ \Delta_{\textrm{air}} = \begin{cases} \delta_{\textrm{air}} & \textrm{if the pass is caught} \\ \Delta & \textrm{if the pass is incomplete,} \end{cases} \] and \[ \Delta_{\textrm{yac}} = \begin{cases} \delta_{\textrm{yac}} & \textrm{if the pass is caught} \\ 0 & \textrm{if the pass is incomplete.} \end{cases} \]

Modeling \(\Delta_{\textrm{air}}\)

\[ \begin{align} \Delta_{i, \textrm{air}} &= Q_{q[i]} + C_{c[i]} + D_{d[i]} + \boldsymbol{\mathbf{x}}_{i}^{\top}\boldsymbol{\beta} + \epsilon_{i}\\ Q_{q} &\sim N(\mu_{Q}, \sigma^{2}_{Q})\\ C_{c} &\sim N(\mu_{C}, \sigma^{2}_{C})\\ D_{d} &\sim N(\mu_{D}, \sigma^{2}_{D}). \end{align} \]

• Fixed effects include:
  • air_yards, shotgun, qb_hit, no_huddle
  • postteam_type (i.e. Home/Away), pass_location
  • receiver_position & rush_strength
• Random intercepts for Quarterback, reCeiver, and Defense

Air Model Results

library(lme4)

air_model <-
  lmer(Delta_air ~ 1 + (1|passer_player_id) + (1 | receiver_player_id) + (1 | defteam )
       + air_yards + shotgun + qb_hit + no_huddle + posteam_type + pass_location + receiver_position + rush_strength,
       data = pass2024)
summary(air_model)

Linear mixed model fit by REML ['lmerMod']
Formula: Delta_air ~ 1 + (1 | passer_player_id) + (1 | receiver_player_id) +  
    (1 | defteam) + air_yards + shotgun + qb_hit + no_huddle +  
    posteam_type + pass_location + receiver_position + rush_strength
   Data: pass2024

REML criterion at convergence: 56640.3

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-9.6663 -0.4475 -0.0140  0.4521  4.2381 

Random effects:
 Groups             Name        Variance Std.Dev.
 receiver_player_id (Intercept) 0.011544 0.10745 
 passer_player_id   (Intercept) 0.002242 0.04735 
 defteam            (Intercept) 0.001354 0.03680 
 Residual                       1.622752 1.27387 
Number of obs: 17000, groups:  
receiver_player_id, 492; passer_player_id, 99; defteam, 32

Fixed effects:
                     Estimate Std. Error t value
(Intercept)         -2.642055   0.573232  -4.609
air_yards            0.035027   0.001077  32.537
shotgun             -0.081497   0.028132  -2.897
qb_hit              -0.276667   0.036182  -7.647
no_huddle            0.134666   0.029805   4.518
posteam_typehome    -0.008663   0.019728  -0.439
pass_locationmiddle  0.172170   0.026424   6.516
pass_locationright  -0.034797   0.022336  -1.558
receiver_positionDL  4.627420   1.401649   3.301
receiver_positionLB  3.750986   1.070748   3.503
receiver_positionOL  2.527147   0.729736   3.463
receiver_positionQB  3.661843   0.934966   3.917
receiver_positionRB  1.922465   0.573394   3.353
receiver_positionTE  2.279044   0.573261   3.976
receiver_positionWR  2.254500   0.573040   3.934
rush_strength        0.307995   0.118268   2.604

Model Interpretation

• \(Q_{q}\) : Per-pass EP added through air by passer \(q\) after adjusting for fixed effects
• \(C_{c}\): per-pass EP added when ball in air by receiver \(c\) after adjusting for fixed effects
• \(D_{d}\): per-pass EP added by offensive team when ball in air while facing defense \(d\)
  • Negative \(D_{d}\) are good for the defense!
• Model: \(Q_{q}, C_{c}\) and \(D_{d}\) noisy deviations from league-wide averages \(\mu_{Q}, \mu_{C},\) and \(\mu_{D}.\)

• Cannot estimate the individual \(Q_{q}\)’s, \(C_{c}\)’s, or \(D_{d}\)’s
• Cannot estimate the global averages \(\mu_{Q}, \mu_{C},\) or \(\mu_{D}\)
• These parameters are not identifiable with the data alone
• Luckily: we can estimate deviations (e.g., \(Q_{q} - \mu_{Q}\))

Individual Points Added over Average

• Definition
• Code
• Top & Bottom 5 Passers

• For passer \(q\), let \(\textrm{IPA}^{(Q)}_{\textrm{air}, q} = Q_{q} - \mu_{Q}\)
  • How much more EP does \(q\) add per play than league-average
• Similarly \(\textrm{IPA}^{(C)}_{\textrm{air}, c}\) and \(\textrm{IPA}^{(D)}_{\textrm{air}, d}.\)

tmp_air <- ranef(air_model) 

air_passer_effects <-
  data.frame(
    gsis_id = rownames(tmp_air[["passer_player_id"]]), 
    ipa_air_pass = tmp_air[["passer_player_id"]][,1])
air_receiver_effects <-
  data.frame(
    gsis_id = rownames(tmp_air[["receiver_player_id"]]),
    ipa_air_rec = tmp_air[["receiver_player_id"]][,1])
air_defense_effects <-
  data.frame(
    Team = rownames(tmp_air[["defteam"]]),
    tpa_air_def = tmp_air[["defteam"]][,1])

air_passer_effects |>
  dplyr::inner_join(y = roster2024 |> dplyr::select(gsis_id, full_name), by = "gsis_id") |>
  dplyr::select(full_name, ipa_air_pass) |>
  dplyr::arrange(dplyr::desc(ipa_air_pass)) |>
  dplyr::slice(c(1:5, (dplyr::n()-4):dplyr::n()))

                  full_name ipa_air_pass
1                Joe Burrow   0.06736333
2               Sam Darnold   0.04033663
3             Lamar Jackson   0.03292716
4            Tua Tagovailoa   0.03281935
5               Brock Purdy   0.03000549
6                 Drew Lock  -0.02737783
7                    Bo Nix  -0.02808707
8  Dorian Thompson-Robinson  -0.03832239
9           Spencer Rattler  -0.05005097
10       Anthony Richardson  -0.07074920

Modeling \(\Delta_{\textrm{yac}}\)

• Fit a nearly-identical multilevel model using only completed passes

completions <-
  pass2024 |>
  dplyr::filter(complete_pass==1)

yac_model <-
  lmer(Delta_yac ~ 1 + (1|passer_player_id) + (1 | receiver_player_id) + (1 | defteam ) 
       + air_yards + shotgun + qb_hit + no_huddle + posteam_type + pass_location + receiver_position + rush_strength, 
       data = completions)

Dealing with Singularities

• Estimated no passer-to-passer variation
• Intuitive: once catch is made, who threw it doesn’t make a difference in terms of EPA.

Linear mixed model fit by REML ['lmerMod']
Formula: Delta_yac ~ 1 + (1 | passer_player_id) + (1 | receiver_player_id) +  
    (1 | defteam) + air_yards + shotgun + qb_hit + no_huddle +  
    posteam_type + pass_location + receiver_position + rush_strength
   Data: completions

REML criterion at convergence: 32367.4

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-8.9533 -0.5437 -0.2533  0.2882  7.4637 

Random effects:
 Groups             Name        Variance  Std.Dev.
 receiver_player_id (Intercept) 0.0190108 0.1379  
 passer_player_id   (Intercept) 0.0000000 0.0000  
 defteam            (Intercept) 0.0006814 0.0261  
 Residual                       0.9296857 0.9642  
Number of obs: 11627, groups:  
receiver_player_id, 468; passer_player_id, 90; defteam, 32

Fixed effects:
                     Estimate Std. Error t value
(Intercept)          1.710173   0.689922   2.479
air_yards           -0.022666   0.001214 -18.675
shotgun             -0.046899   0.025546  -1.836
qb_hit               0.037119   0.039172   0.948
no_huddle           -0.174386   0.027107  -6.433
posteam_typehome    -0.007157   0.018083  -0.396
pass_locationmiddle -0.057884   0.024339  -2.378
pass_locationright   0.011441   0.020532   0.557
receiver_positionDL -1.567487   1.193518  -1.313
receiver_positionLB -0.728621   0.974493  -0.748
receiver_positionOL -1.046652   0.781368  -1.340
receiver_positionQB -0.728794   0.974704  -0.748
receiver_positionRB -0.515251   0.689574  -0.747
receiver_positionTE -0.837277   0.689576  -1.214
receiver_positionWR -0.847828   0.689446  -1.230
rush_strength        0.382583   0.105680   3.620

optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')

Computing IPA for YAC

• Using ranef, we can extract YAC-specific IPAs for passers, receivers, and defenses
• Top-10 based on \(\textrm{IPA}^{(C)}_{\textrm{yac}, c}\) contains many well-known receivers

         full_name ipa_yac_rec
1  Marvin Mims Jr.   0.4038113
2    Khalil Shakir   0.2763021
3  KaVontae Turpin   0.2225070
4    Xavier Worthy   0.2179003
5     Tucker Kraft   0.2141390
6     Brock Bowers   0.1885809
7    Austin Ekeler   0.1830305
8   Antonio Gibson   0.1818104
9    Ja'Marr Chase   0.1778265
10  Raheem Mostert   0.1729994

Rushing Model

Handling QB Runs

• Play-by-play data doesn’t distinguish between
  • Designed QB runs
  • Scrambles on broken plays
• We will fit two separate models for EPA on rushing plays

qb_runs <-
  rush2024 |>
  dplyr::filter(rusher_position == "QB")

nonqb_runs <-
  rush2024 |>
  dplyr::filter(rusher_position != "QB")

Multilevel Models

• Overview
• Code
• Top \(\textrm{IPA}^{(R)}_{r}\) Values

• QB Run Model:
  • Fixed effects: shotgun, no_huddle, posteam_type, pass_strength
  • Random intercepts: rusher_player_id & defteam
• Non-QB Model
  • Fixed effects: same as QB-model + rusher_position & run_context
  • Random intercepts: same as QB-model
• Use ranef() to extract \(\textrm{IPA}^{(R)}_{r}\) for Runner r

qbrun_fit <-
  lmer(epa ~ 1 + (1 | rusher_player_id) + (1 | defteam) +
         shotgun + no_huddle + posteam_type + pass_strength,
       data = qb_runs)
nonqb_run_fit <-
  lmer(epa ~ 1 + (1 | rusher_player_id) + (1 | defteam) +  
         shotgun + no_huddle + posteam_type + rusher_position + run_context + pass_strength,
       data = nonqb_runs)

         full_name    ipa_run
1    De'Von Achane 0.13626662
2   Saquon Barkley 0.10131412
3     Jahmyr Gibbs 0.09383069
4      Jerome Ford 0.08473154
5    Chuba Hubbard 0.08423388
6     J.K. Dobbins 0.07766485
7  Emari Demercado 0.07656891
8    Dameon Pierce 0.06755530
9      Rico Dowdle 0.06517368
10     Taysom Hill 0.06219509

Creating NFL WAR

Total Individual Points Added Above Average

• For every offensive player, estimate how more EP they add per-play than league-average
  • Through the air (\(\textrm{IPA}^{(Q)}_{\textrm{air}, q}\), \(\textrm{IPA}^{(C)}_{\textrm{air}, c}\))
  • After the catch (\(\textrm{IPA}^{(Q)}_{\textrm{yac}, q}\), \(\textrm{IPA}^{(C)}_{\textrm{yac}, c}\))
  • Rushing (\(\textrm{IPA}^{(R)}_{r}\))
• Multiplying \(\textrm{IPA}\) by number of attempts yields \(\textrm{IPAA}\): total points added above average

Computing IPAA

• Code
• Passers
• Receivers
• QB Rushing
• Non-QB Rushing

passer_ipaa <-
  pass2024 |>
  dplyr::group_by(passer_player_id) |> 
  dplyr::summarise(n_pass = dplyr::n()) |>
  dplyr::rename(gsis_id = passer_player_id) |> 
  dplyr::left_join(air_passer_effects, by = "gsis_id") |> 
  dplyr::left_join(yac_passer_effects, by = "gsis_id") |> 
  dplyr::mutate(
    ipaa_air_pass = ipa_air_pass * n_pass,
    ipaa_yac_pass = ipa_yac_pass * n_pass) |>
  dplyr::left_join(y = roster2024 |> dplyr::select(gsis_id, full_name, position), by = "gsis_id")

passer_ipaa |>
  dplyr::select(full_name, n_pass, ipa_air_pass, ipa_yac_pass, ipaa_air_pass, ipaa_yac_pass) |>
  dplyr::arrange(dplyr::desc(ipaa_air_pass)) |>
  dplyr::slice_head(n = 10)

# A tibble: 10 × 6
   full_name      n_pass ipa_air_pass ipa_yac_pass ipaa_air_pass ipaa_yac_pass
   <chr>           <int>        <dbl>        <dbl>         <dbl>         <dbl>
 1 Joe Burrow        628       0.0674            0         42.3              0
 2 Sam Darnold       512       0.0403            0         20.7              0
 3 Lamar Jackson     454       0.0329            0         14.9              0
 4 Brock Purdy       440       0.0300            0         13.2              0
 5 Tua Tagovailoa    388       0.0328            0         12.7              0
 6 Justin Herbert    484       0.0262            0         12.7              0
 7 Baker Mayfield    562       0.0198            0         11.1              0
 8 C.J. Stroud       509       0.0166            0          8.45             0
 9 Russell Wilson    306       0.0231            0          7.07             0
10 Geno Smith        554       0.0110            0          6.07             0

# A tibble: 10 × 6
   full_name         n_rec ipa_air_rec ipa_yac_rec ipaa_air_rec ipaa_yac_rec
   <chr>             <int>       <dbl>       <dbl>        <dbl>        <dbl>
 1 Tee Higgins         109      0.182     -0.0741          19.9       -8.07 
 2 Amon-Ra St. Brown   141      0.139      0.0563          19.6        7.93 
 3 Ladd McConkey       112      0.148     -0.0124          16.5       -1.38 
 4 Terry McLaurin      117      0.118     -0.0612          13.7       -7.16 
 5 DeVonta Smith        89      0.142     -0.0383          12.7       -3.41 
 6 Jauan Jennings      113      0.111     -0.118           12.6      -13.3  
 7 Jakobi Meyers       129      0.0928     0.00289         12.0        0.373
 8 Justin Jefferson    153      0.0746     0.0566          11.4        8.66 
 9 Courtland Sutton    135      0.0812    -0.156           11.0      -21.1  
10 Jonnu Smith         111      0.0910     0.166           10.1       18.4  

# A tibble: 10 × 4
   full_name          ipa_qbrun n_qbrun ipaa_qbrun
   <chr>                  <dbl>   <int>      <dbl>
 1 Jayden Daniels         0.469     184       86.3
 2 Josh Allen             0.703     108       75.9
 3 Anthony Richardson     0.667      94       62.7
 4 Jalen Hurts            0.307     167       51.3
 5 Bo Nix                 0.481     102       49.1
 6 Lamar Jackson          0.322     150       48.2
 7 Kyler Murray           0.336     102       34.3
 8 Brock Purdy            0.319      92       29.4
 9 Patrick Mahomes        0.344      74       25.5
10 Daniel Jones           0.283      88       24.9

# A tibble: 10 × 4
   full_name      ipa_run n_run ipaa_run
   <chr>            <dbl> <int>    <dbl>
 1 Saquon Barkley  0.101    346     35.1
 2 De'Von Achane   0.136    203     27.7
 3 Jahmyr Gibbs    0.0938   250     23.5
 4 Chuba Hubbard   0.0842   250     21.1
 5 Derrick Henry   0.0520   325     16.9
 6 Rico Dowdle     0.0652   235     15.3
 7 J.K. Dobbins    0.0777   195     15.1
 8 Bijan Robinson  0.0477   304     14.5
 9 Najee Harris    0.0481   263     12.7
10 Chase Brown     0.0505   229     11.6

Replacement Level

• Multilevel models involved global-averages \(\mu_{Q}, \mu_{C}, \mu_{R}\)
  • Represent the average latent intercept across theoretical super-population
  • Assumption: observed players are randomly sampled from this super-population
• Not strictly correct to say IPA measures contribution above “league-average”

• Will define roster-based thresholds for “replacement level”
• Construct a replacement-level “shadow”
  • Compute average \(\textrm{IPA}\) for replacement-level players
  • Shadow IPAA: multiply avg. replacement-level IPA by attempts
  • Compare observed IPAA to shadow IPAA

Defining Replacement Level

• Most rosters: 3 running backs, 4 wide receivers, 2 tight ends

• Create separate thresholds for position & type of play

• For passing plays:

  • Top \(32 \times 4\) WRs sorted by n_rec
  • Top \(32 \times 2\) TEs sorted by n_rec
  • Top \(32 \times 3\) RB

• For running plays

  • Top \(32 \times 3\) RBs sorted by n_runs
  • Top \(32 \times 1\) WR & TEs sorted by n_runs

Running IPAR

• Threshold
• Players
• Replacement IPA
• Shadow

rb_run_threshold <- run_ipaa |> 
  dplyr::filter(position == "RB") |>
  dplyr::arrange(desc(n_run)) |>
  dplyr::slice(96) |>
  dplyr::pull(n_run)

wrte_run_threshold <- run_ipaa |>
  dplyr::filter(position %in% c("WR", "TE")) |>
  dplyr::arrange(desc(n_run)) |>
  dplyr::slice(32) |>
  dplyr::pull(n_run)

run_ipaa <- 
  run_ipaa |>
  dplyr::mutate(
    repl_wrte = dplyr::case_when(
      position %in% c("WR", "TE") & n_run < wrte_run_threshold ~ 1,
      position %in% c("WR", "TE") & n_run >= wrte_run_threshold ~ 0,
      !position %in% c("WR", "TE") ~ NA),
    repl_rb = dplyr::case_when(
      position == "RB" & n_run < rb_run_threshold ~ 1,
      position == "RB" & n_run >= rb_run_threshold ~ 0,
      position != "RB" ~ NA))

• Compute average IPA for all replacement-level players

repl_wrte_ipa_run <-  run_ipaa |>
  dplyr::filter(repl_wrte == 1) |>
  dplyr::pull(ipa_run) |>
  mean(na.rm = TRUE)

repl_rb_ipa_run <- run_ipaa |>
  dplyr::filter(repl_rb == 1) |>
  dplyr::pull(ipa_run) |>
  mean(na.rm = TRUE)

run_ipar <- run_ipaa |>
  dplyr::filter(position %in% c("WR", "RB", "TE")) |>
   dplyr::mutate(
    shadow_run = dplyr::case_when(
      position %in% c("WR", "TE") ~ n_run * repl_wrte_ipa_run,
      position == "RB" ~ n_run * repl_rb_ipa_run),
    ipar_run = ipaa_run - shadow_run)

# A tibble: 10 × 3
   full_name      ipaa_run ipar_run
   <chr>             <dbl>    <dbl>
 1 Saquon Barkley     35.1     38.5
 2 De'Von Achane      27.7     29.7
 3 Jahmyr Gibbs       23.5     25.9
 4 Chuba Hubbard      21.1     23.5
 5 Derrick Henry      16.9     20.1
 6 Rico Dowdle        15.3     17.6
 7 Bijan Robinson     14.5     17.5
 8 J.K. Dobbins       15.1     17.1
 9 Najee Harris       12.7     15.2
10 Chase Brown        11.6     13.8

Computing Remaining IPAR’s

• Virtually same process for both passing IPAR’s
• Top 10 YAC IPAR

# A tibble: 10 × 3
   full_name        ipaa_yac_rec ipar_yac_rec
   <chr>                   <dbl>        <dbl>
 1 Ja'Marr Chase            31.1         31.3
 2 Brock Bowers             28.9         30.2
 3 Khalil Shakir            27.6         27.7
 4 DJ Moore                 22.5         22.6
 5 Brian Thomas Jr.         22.4         22.5
 6 Xavier Worthy            21.4         21.4
 7 Marvin Mims Jr.          21.0         21.0
 8 Jonnu Smith              18.4         19.4
 9 Puka Nacua               16.4         16.4
10 Tucker Kraft             14.8         15.4

Replacement-level QB

• Every offensive play runs through the QB
• Idea 1: designate one QB per team as non-replacement
  • E.g., QB w/ most rushing & passing attempts
  • Problem: assumes every NFL team has at least one non-replacement QB
• Idea 2: sort QBs by total number of passes & rushes & take top-32
• Top-10 IPAR via passing

# A tibble: 10 × 3
   full_name      ipa_air_pass ipar_air_pass
   <chr>                 <dbl>         <dbl>
 1 Joe Burrow           0.0674         44.6 
 2 Sam Darnold          0.0403         22.6 
 3 Lamar Jackson        0.0329         16.6 
 4 Brock Purdy          0.0300         14.8 
 5 Justin Herbert       0.0262         14.5 
 6 Tua Tagovailoa       0.0328         14.2 
 7 Baker Mayfield       0.0198         13.2 
 8 C.J. Stroud          0.0166         10.4 
 9 Russell Wilson       0.0231          8.21
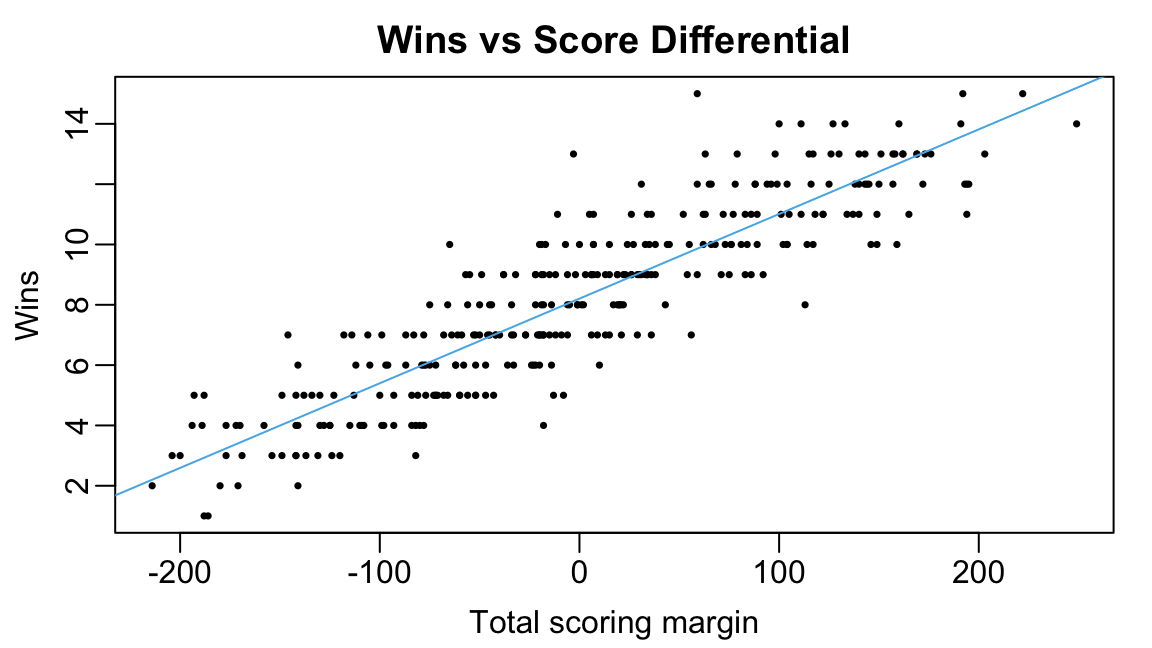
10 Geno Smith           0.0110          8.13

Converting Points to Wins

• IPAR are on point-differential scale
• Find \(\alpha\) & \(\beta\) s.t. \(\textrm{Wins} \approx \alpha + \beta \times \textrm{PtsDiff}\)
• Then multiply IPAR values by \(\beta\)

Figure 1: Scoring differential is positively associated with wins

Skill-Position WAR

• Convert each IPAR to wins scale & then sum
• Top-10 Skill Positions

           full_name       war
1      De'Von Achane 1.2408245
2     Saquon Barkley 1.1551989
3      Ja'Marr Chase 1.0545348
4       Jahmyr Gibbs 0.8666242
5        Jonnu Smith 0.8446721
6  Amon-Ra St. Brown 0.8086111
7       Brock Bowers 0.7438843
8      Derrick Henry 0.6381019
9         Puka Nacua 0.6084343
10  Justin Jefferson 0.6012925

Reminders

• Project reports & presentations due at 12pm (noon) on Friday

• Please also upload recording to shared Box folder (link on Canvas)

• I’ll announce peer review assignments by Thursday night

  • You must review 3 reports & presentations of 3 other teams
  • Due on 10/17
  • Rubric + constructive comments