STAT 479: Lecture 8

Defensive Credit & WAR

Recap & Overview

Offensive Credit Allocation

  • During at-bat \(i\), batting team generates \(\delta_{i}\) run value
  • Lecture 7: divide \(\delta_{i}\) b/w batter and baserunners
  • Conservation of run value: if batting team gains \(\delta\), fielding team gains \(-\delta\)
  • Today: divide \(-\delta_{i}\) b/w pitcher and fielders

Two Possibilities

  • Ball is not put in play during at-bat
    • At-bat ends w/ homerun, strikeout, walk
    • Pitcher deserves all credit (or blame)
  • Ball is put in play (e.g., flyout, groundout, single, double, triple, etc.)
    • \(\hat{p}\): probability of making an out (based on location)
    • Give \(\delta^{(p)} = -\delta \times (1-\hat{p})\) to the pitcher
    • Divide \(\delta^{(f)} = -\delta \times \hat{p}\) among other fielders

Data Preparation

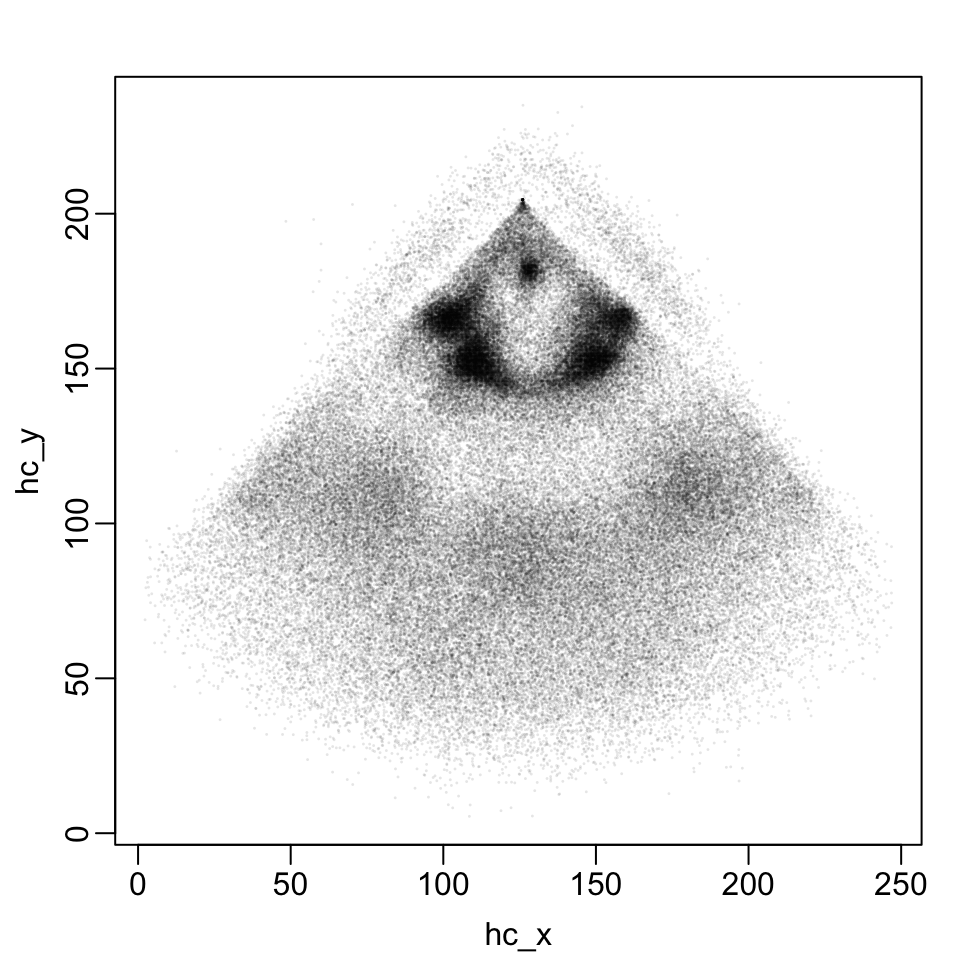
Statcast Coordinates

  • hc_x and hc_y: coordinates where batted ball is first fielded
  • hit_location: position of player who first fielding ball
  • Statcast coordinate system
    • Home plate at top of plot near (125, 200)
    • First baseline on the left
    • Units are not in feet
Figure 1: Locations where all batted balls are first fielded
Figure 2: Location of all batted balls initially fielded by the first baseman

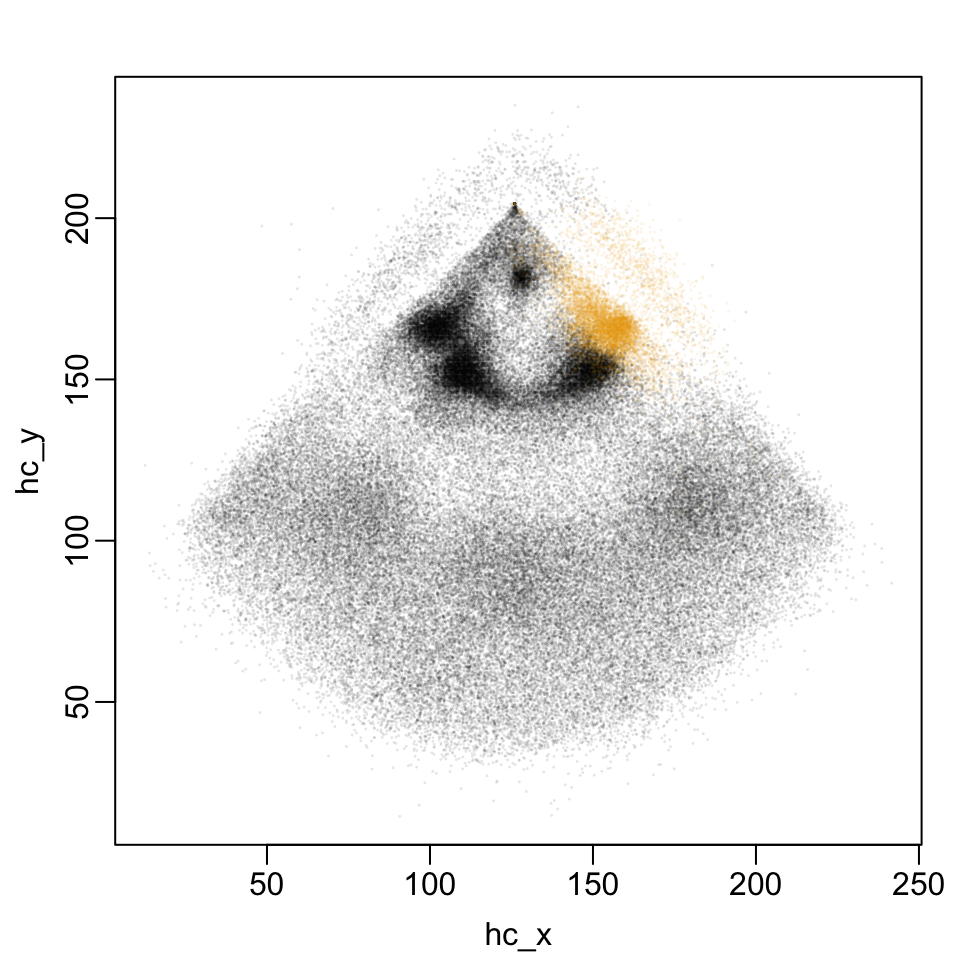
Transformed Coordinates

  • Transform: x = 2.5 * (hc_x - 125.42) & y = 2.5 * (198.27 - hc_y)
  • Define new coordinate system where
    • Home plate at bottom of plot at (0,0)
    • Units are in feet
    • First base on the right around (90/sqrt(2), 90/sqrt(2))
Figure 3: New coordinate system

More Data Preparation

  • def_atbat2024: at-bat level data table containing
    • Pitcher & fielder identities
    • Batted ball locations & fielder position
    • Ending values of type and events: i.e. end_type and end_events
      • Useful for determining at-bat level outcomes
    • Narrative descriptions: des
  • See lecture notes for full code

Estimating Out Probabilities

Unique Events I

  • end_type: did last pitch of at-bat end in Strike, Ball, or contact (X)?

  • events: more granular description of at-bat outcome

  • All events when contact is made

table(def_atbat2024$end_events[def_atbat2024$end_type == "X"], useNA = 'always')

                   double               double_play               field_error 
                     7608                       336                      1093 
                field_out           fielders_choice       fielders_choice_out 
                    72233                       373                       306 
                force_out grounded_into_double_play                  home_run 
                     3408                      3152                      5326 
                 sac_bunt                   sac_fly       sac_fly_double_play 
                      446                      1222                        13 
                   single                    triple               triple_play 
                    25363                       685                         1 
                     <NA> 
                        0

Unique Events II

  • All events for balls and strikes
table(def_atbat2024$end_events[def_atbat2024$end_type != "X"], useNA = 'always')

                             catcher_interf          hit_by_pitch 
                  308                    97                  1977 
            strikeout strikeout_double_play          truncated_pa 
                40145                   107                   304 
                 walk                  <NA> 
                14029                     0

Extract Balls in Play

  • Some manual correction was needed
bip <- def_atbat2024 |> dplyr::filter(end_type == "X")
bip$end_events[65138] <- "fielders_choice_out"
out_events <- 
  c("double_play", "field_out", "fielders_choice_out",
    "force_out", "grounded_into_double_play", 
    "sac_bunt", "sac_fly", "sac_fly_double_play",
    "triple_play")
bip <-
  bip |>
  dplyr::filter(end_events != "home_run" & !is.na(x) & !is.na(y)) |>
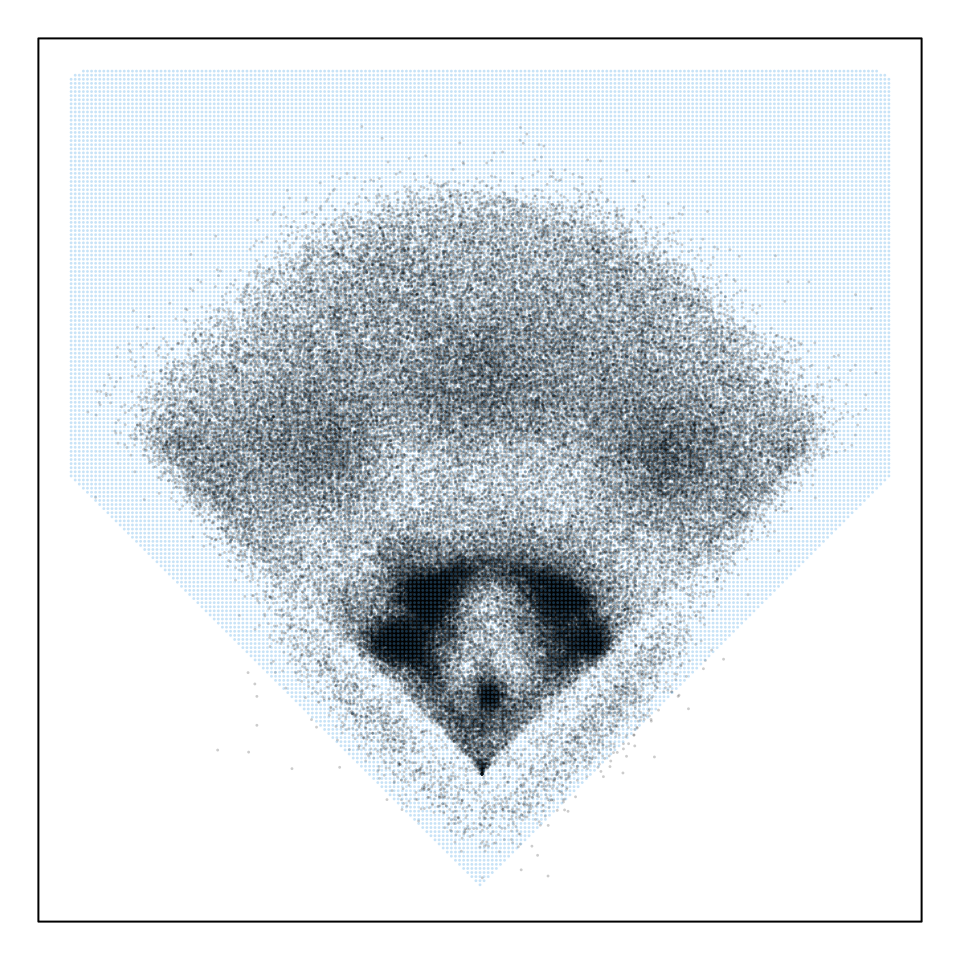
  dplyr::mutate(Out = ifelse(end_events %in% out_events, 1, 0))

Binning & Averaging

  • Divide field into grid of 3ft x 3ft bins
  • Remove unrealistic grid locations
grid_sep <- 3 
x_grid <- seq(from = -300, to = 300, by = grid_sep)
y_grid <- seq(from = -100, to = 500, by = grid_sep)
raw_grid <- expand.grid(x = x_grid, y = y_grid)

grid <- raw_grid |>
  dplyr::filter(y + x > -100 & y - x > -100 & sqrt(x^2 + y^2) < 580)
Figure 4: Restricted grid of spatial locations 
bin_probs <-
  bip |>
  dplyr::select(x, y, Out) |>
  dplyr::mutate(
    x_bin = cut(x, breaks = seq(-300-grid_sep/2, 300+grid_sep/2, by = grid_sep)), 
    y_bin = cut(y, breaks = seq(-100 - grid_sep/2, 500+grid_sep/2, by = grid_sep))) |>
  dplyr::group_by(x_bin, y_bin) |>
  dplyr::summarise(
    out_prob = mean(Out), 
    n_balls = dplyr::n(),
    .groups = "drop")
Figure 5: Empirical out probabilities based on binning balls in play.

Logistic Regression

  • What about a logistic regression model? \[ \log\left(\frac{\mathbb{P}(\textrm{out})}{1 - \mathbb{P}(\textrm{out})}\right) = \beta_{0} + \beta_{1}x + \beta_{2}y \]
logit_fit <-
  glm(Out ~ x + y,
      family = binomial(link = "logit"), data = bip)

Logistic Regression Estimates

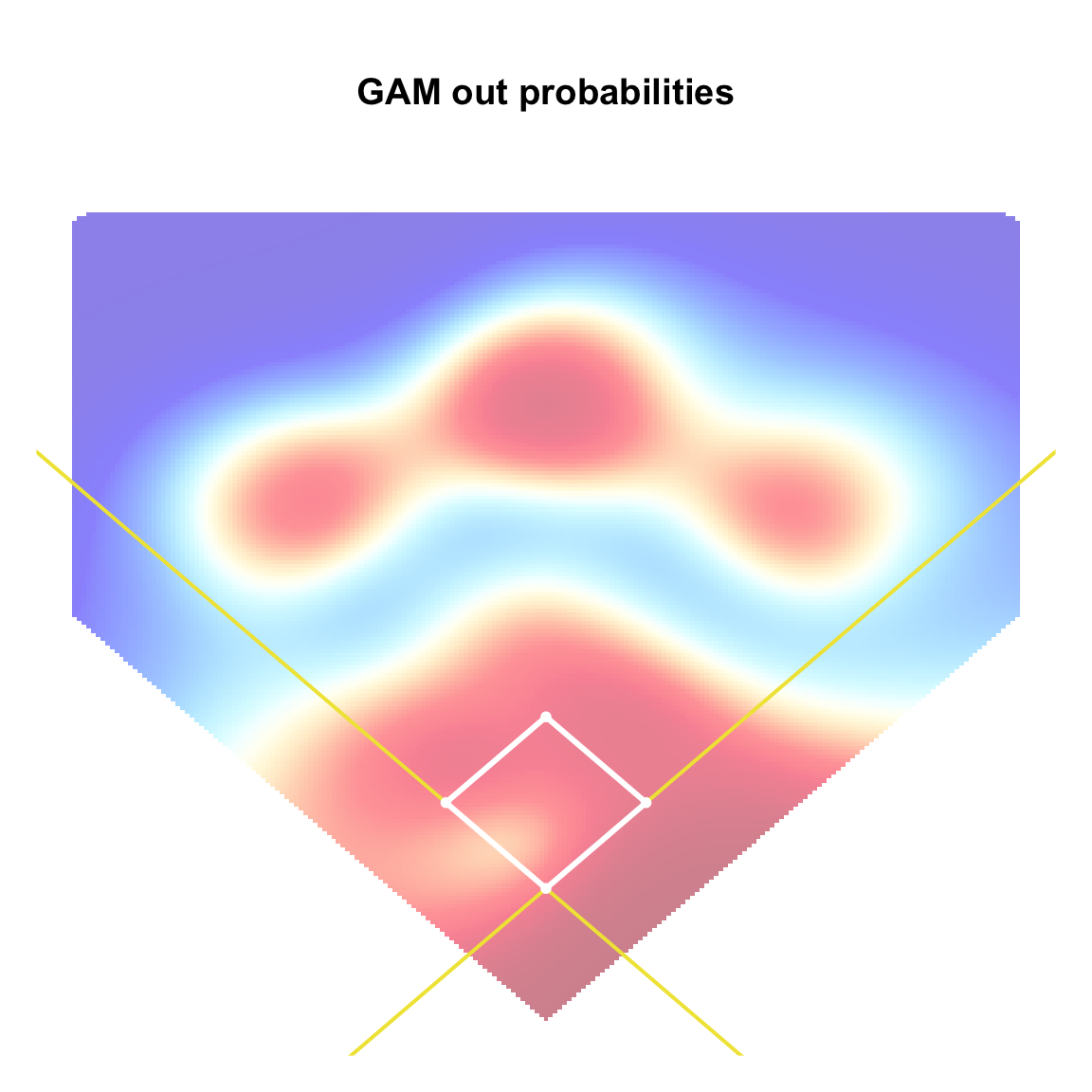
Figure 6: Logistic regression forecasts of out probabilities as a function of location.

Generalized Additive Model

\[ \log\left(\frac{\mathbb{P}(\textrm{out})}{1 - \mathbb{P}(\textrm{out})} \right) = s(x,y), \]

  • \(s(x,y)\) is a smooth function in both \(x\) and \(y\)
    • Technically: \(s(x,y) = \sum_{d=1}^{D}{\beta_{d}\phi_{d}(x,y)}\)
    • \(\phi_{1}, \ldots, \phi_{D}\): fixed set of spline functions
    • \(\phi_{d}\) piecewise polynomial localized to small spatial region
  • Can be fit using the mgcv package

GAM Estimates

  • Use mgcv::bam for large datasets
library(mgcv)
gam_fit <-
  bam(formula = Out ~ s(x,y), 
      family = binomial(link="logit"), data = bip)
Figure 7: GAM-estimated out probabilities 
all_preds <-
  predict(object = gam_fit, 
          newdata = def_atbat2024,
          type = "response")
def_atbat2024$p_out <- all_preds

def_atbat2024 <-
  def_atbat2024 |>
  dplyr::mutate(
    p_out = dplyr::case_when(
      is.na(p_out) & end_events == "home_run" ~ 0, 
      is.na(p_out) & end_type != "X" ~ 0, 
      .default = p_out)) |>
  dplyr::filter(!is.na(p_out))

Defining \(\delta^{(p)}\) and \(\delta^{(f)}\)

  • Divide run value \(\delta\) into
    • \(\delta^{(f)} = -1 \times \hat{p} \times \delta\)
    • \(\delta^{(p)} = -1 \times (1 - \hat{p}) \times \delta\)
def_atbat2024 <-
  def_atbat2024 |>
  dplyr::mutate(
    delta_p = -1 * (1 - p_out) * RunValue,
    delta_f = -1 * p_out * RunValue)

Pitching Run Values

\(\textrm{RAA}^{(p)}\) (definition)

  • \(\delta_{i}^{(p)} = -1 \times (1 - \hat{p}_{i}) \times \delta_{i}\)
    • Run value created by pitcher in at-bat \(i\)
    • Positive values indicate good performance
  • \(\textrm{RAA}^{(p)}\): sum \(\delta_{i}^{(p)}\)’s across each pitchers at-bats

Computing \(\textrm{RAA}^{(p)}\)

raa_p <-
  def_atbat2024 |>
  dplyr::select(pitcher, delta_p) |>
  dplyr::group_by(pitcher) |>
  dplyr::summarise(RAA_p = sum(delta_p, na.rm = TRUE)) |>
  dplyr::rename(key_mlbam = pitcher) |>
  dplyr::inner_join(y = player2024_lookup, by = "key_mlbam") |>
  dplyr::select(Name, key_mlbam, RAA_p)
raa_p |>
  dplyr::arrange(dplyr::desc(RAA_p)) |>
  dplyr::slice_head(n=10)
# A tibble: 10 × 3
   Name            key_mlbam RAA_p
   <chr>               <int> <dbl>
 1 Tarik Skubal       669373 14.7 
 2 Chris Sale         519242 14.6 
 3 Ryan Walker        676254 13.5 
 4 Cade Smith         671922 13.3 
 5 Paul Skenes        694973 12.3 
 6 Emmanuel Clase     661403 11.2 
 7 Kirby Yates        489446  9.99
 8 Griffin Jax        643377  9.53
 9 Edwin Uceta        670955  9.23
10 Garrett Crochet    676979  9.13

Fielding Run Values

Fielding Responsibility

  • Say ball hit towards gap b/w 1st base and right field
    • Batting team creates large positive \(\delta\)
    • \(\hat{p} \approx 0\)
    • \(\delta^{(f)}\) is large and negative
  • How much blame should third baseman receive?

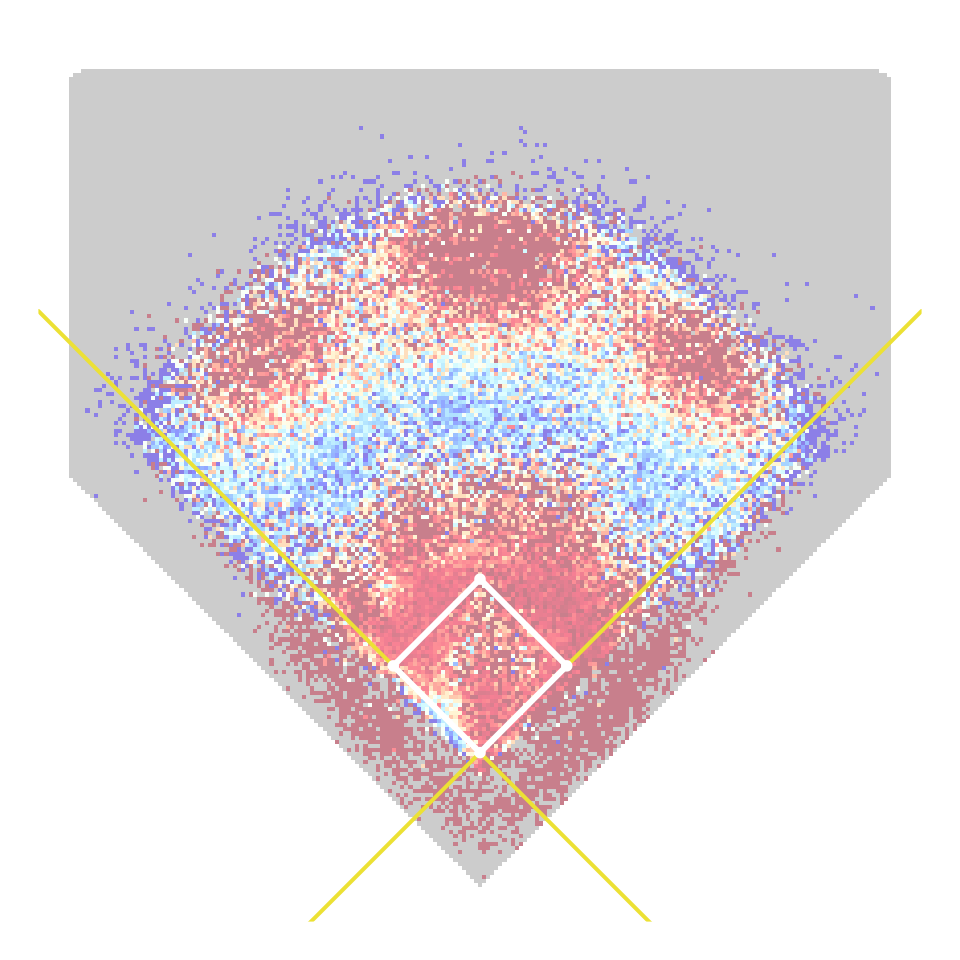
Fielder Out Probabilities

Figure 8
Figure 9

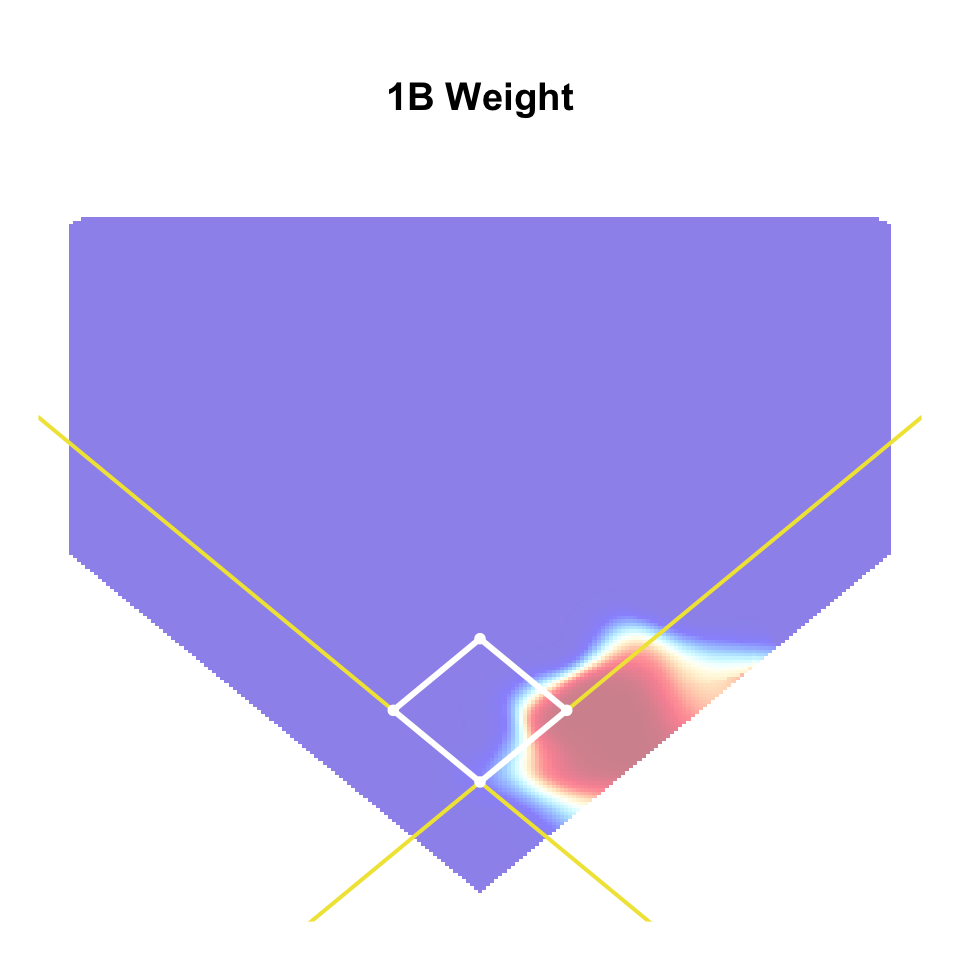
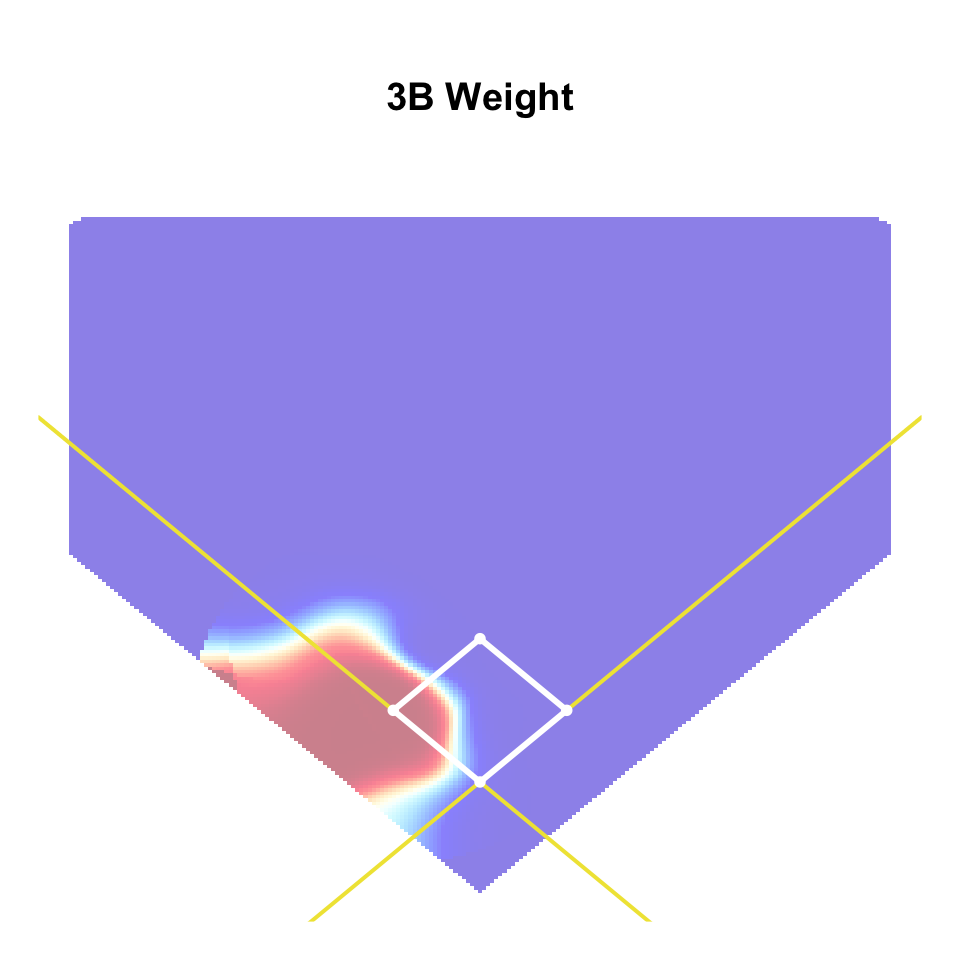
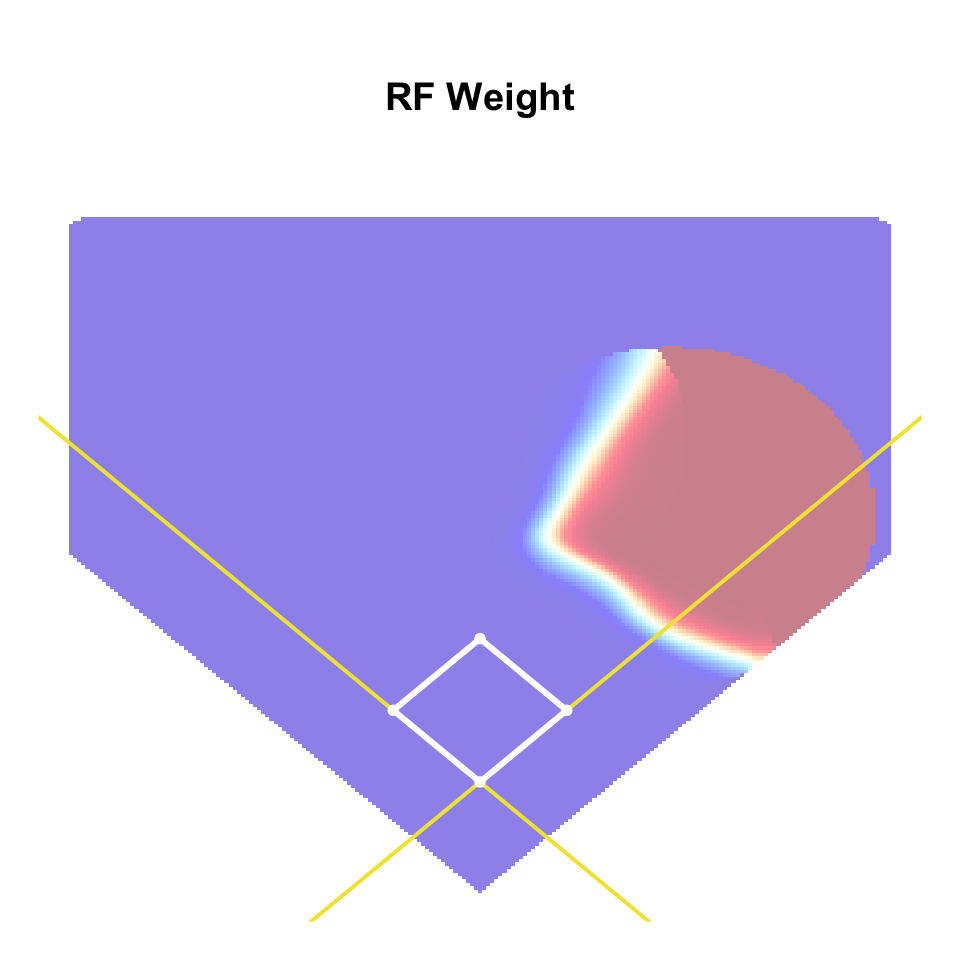
Position Weights

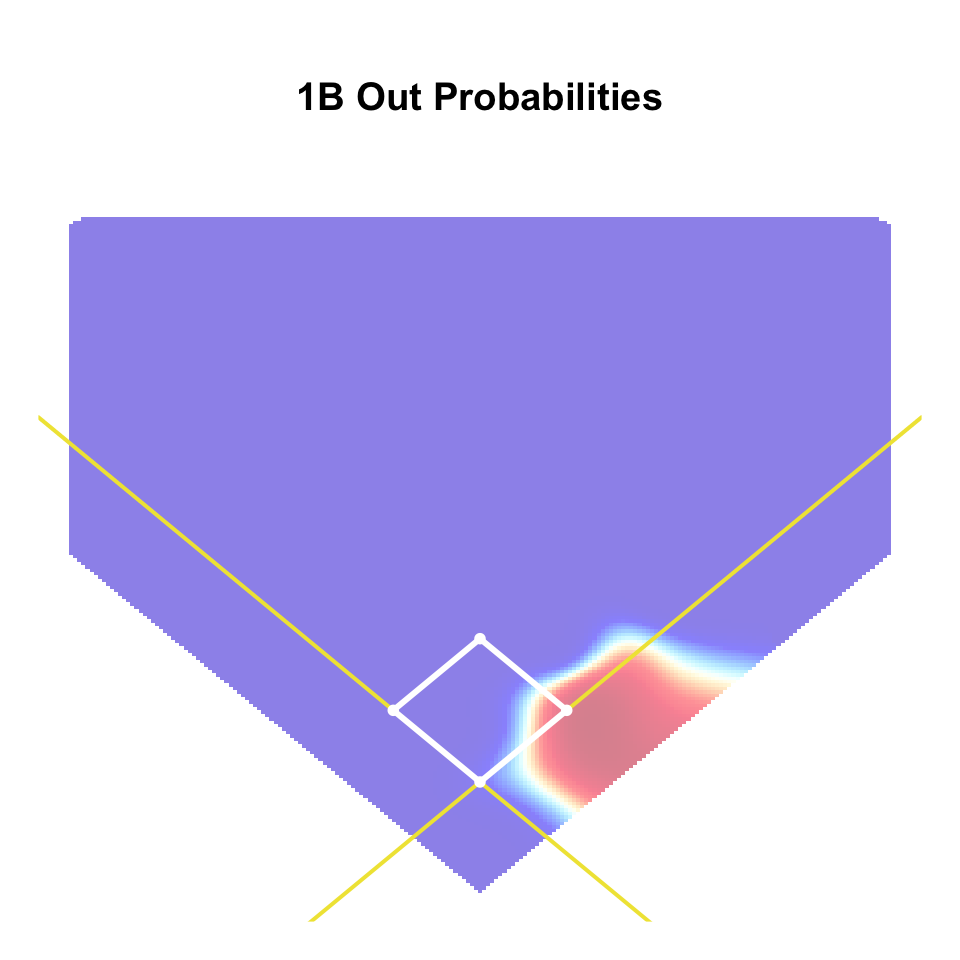
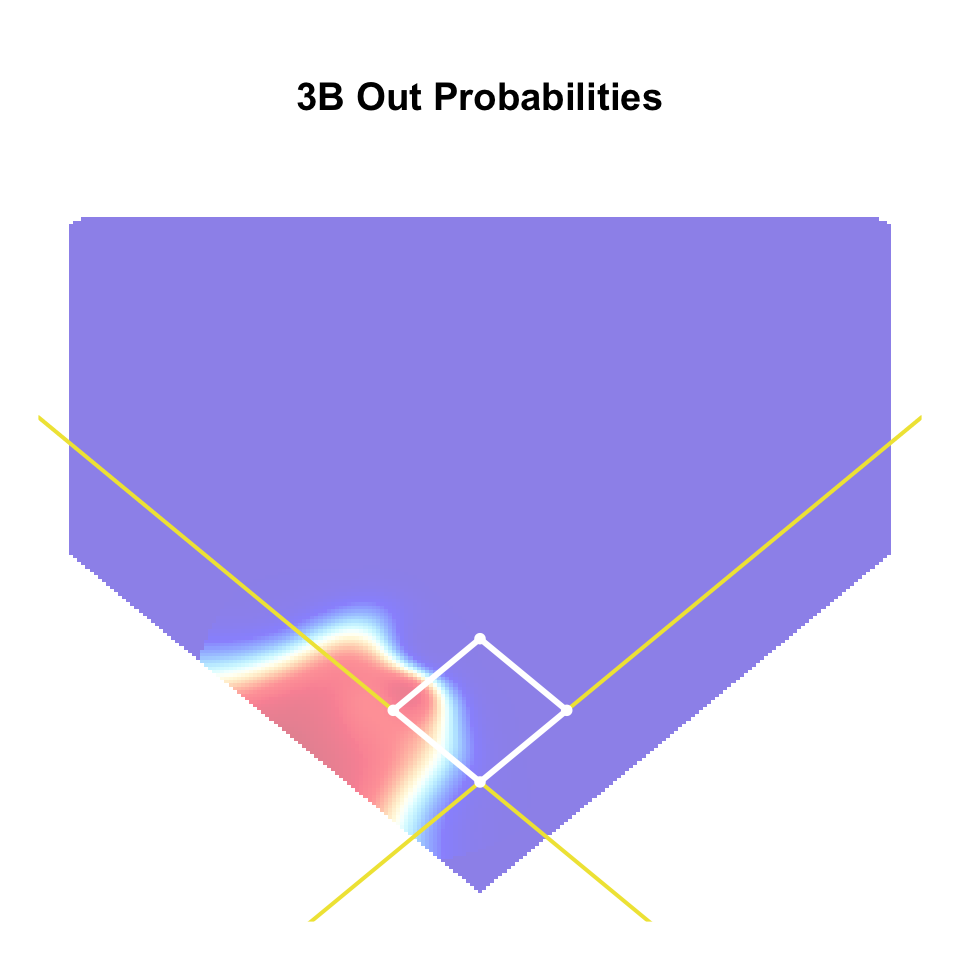
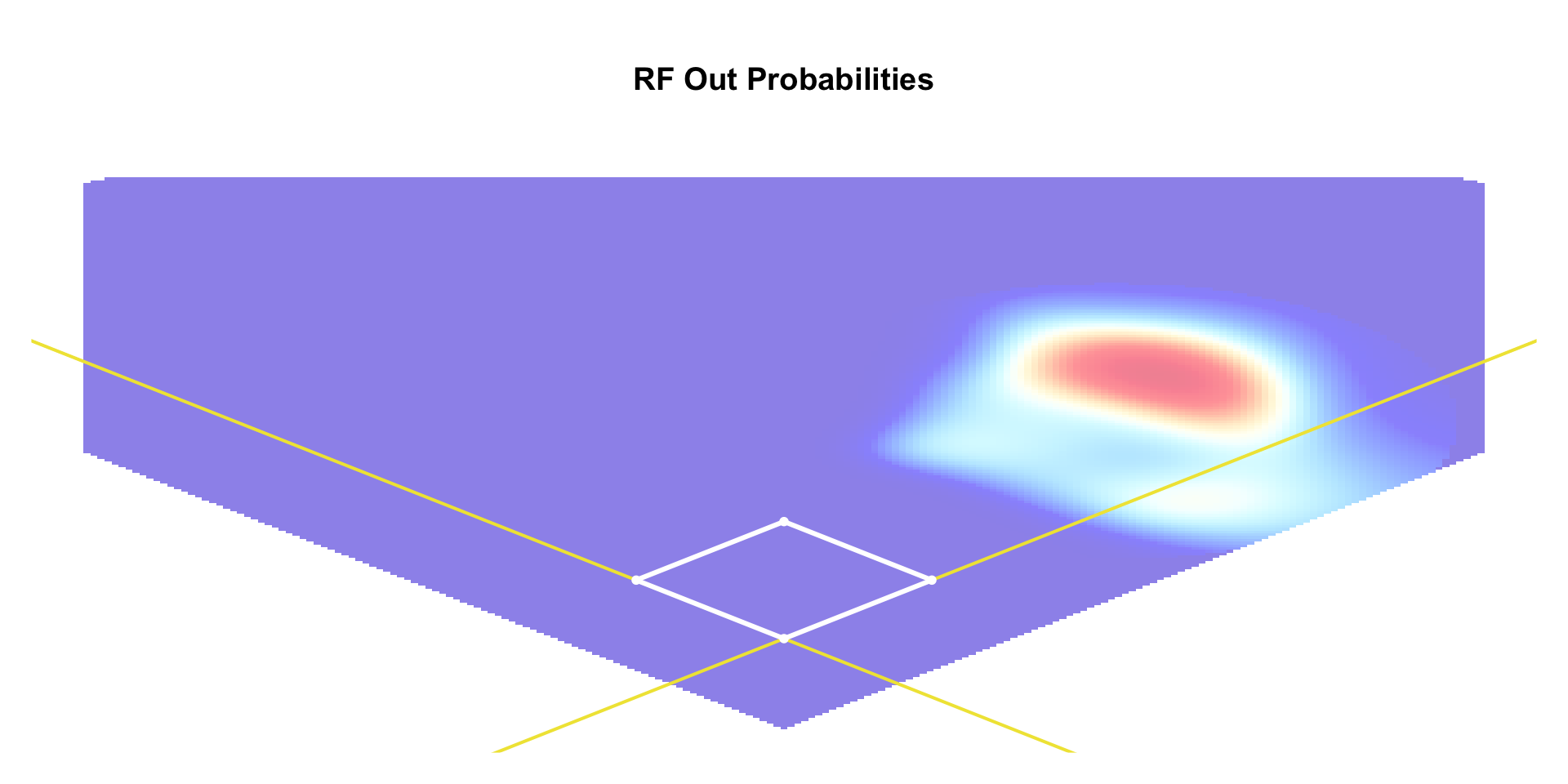
  • Idea: assign \(w_{\ell} \delta^{(f)}\) to fielder at position \(\ell\) \[ w_{\ell} = \frac{\hat{p}_{\ell}}{\hat{p}_{1} + \cdots + \hat{p}_{9}} \]
  • \(\hat{p}_{\ell}\): prob. that fielder position \(\ell\) makes out based on location
  • Can estimate \(\hat{p}_{\ell}\) with fielder-specific GAMs
  • Numerical stability: restrict to balls w/in 150ft of typical fielder location
    • I.e., balls hit to deep left field likely irrelevant for first baseman model

Position Weights Examples

Figure 10
Figure 11
Figure 12

Run Value by Fielding Position

  • For each at-bat \(i\) assign \(w_{i,\ell}\delta_{i}^{(f)}\) to player at position \(\ell\)
  • Sums these values for each player-position to get \(\textrm{RAA}_{\ell}^{(f)}\)
    • Some players play multiple positions in the field
  • \(\textrm{RAA}_{\ell}^{(f)}\): run value created by playing position \(\ell\)
raa_f3 <-
  def_atbat2024 |>
  dplyr::mutate(RAA_f3 = delta_f * w3) |>
  dplyr::group_by(fielder_3) |>
  dplyr::summarize(RAA_f3 = sum(RAA_f3, na.rm = TRUE)) |>
  dplyr::rename(key_mlbam = fielder_3)
raa_f3 |>
  dplyr::inner_join(y = player2024_lookup, by = "key_mlbam") |>
  dplyr::select(Name, RAA_f3) |>
  dplyr::arrange(dplyr::desc(RAA_f3)) |>
  dplyr::slice_head(n = 10)
# A tibble: 10 × 2
   Name              RAA_f3
   <chr>              <dbl>
 1 Carlos Santana      55.7
 2 Christian Walker    54.6
 3 Paul Goldschmidt    52.4
 4 Bryce Harper        51.1
 5 Matt Olson          51.0
 6 Ryan Mountcastle    48.7
 7 Vladimir Guerrero   47.1
 8 Michael Toglia      46.5
 9 Freddie Freeman     46.2
10 Josh Naylor         46.2

Total Fielding Run Value \(\textrm{RAA}^{(f)}\)

  • For each player we have \(\textrm{RAA}^{(f)}_{1}, \ldots, \textrm{RAA}^{(f)}_{9}\)
    • \(\textrm{RAA}^{(f)}_{\ell}\): total run value created from fielding at position \(\ell\)
  • \(\textrm{RAA}^{(f)} = \textrm{RAA}^{(f)}_{1} + \cdots + \textrm{RAA}^{(f)}_{9}\)

Putting It All Together

  • \(\textrm{RAA} = \textrm{RAA}^{(b)} + \textrm{RAA}^{(br)} + \textrm{RAA}^{(f)} + \textrm{RAA}^{(p)}\)
raa <-
  raa_b |>
  dplyr::select(-Name) |>
  dplyr::full_join(y = raa_br |> dplyr::select(-Name), by = "key_mlbam") |>
  dplyr::full_join(y = raa_p |> dplyr::select(-Name), by = "key_mlbam") |>
  dplyr::full_join(y = raa_f |> dplyr::select(-Name), by = "key_mlbam") |>
  tidyr::replace_na(list(RAA_b = 0, RAA_br = 0, RAA_f = 0, RAA_p = 0)) |>
  dplyr::mutate(RAA = RAA_b + RAA_br + RAA_f + RAA_p) |>
  dplyr::left_join(y = player2024_lookup |> dplyr::select(key_mlbam, Name), by = "key_mlbam") |>
  dplyr::select(Name, key_mlbam, RAA, RAA_b, RAA_br, RAA_f, RAA_p)

RAA Leaderboard

# A tibble: 10 × 7
   Name              key_mlbam   RAA  RAA_b RAA_br RAA_f RAA_p
   <chr>                 <dbl> <dbl>  <dbl>  <dbl> <dbl> <dbl>
 1 Bobby Witt           677951 165.  61.1   24.9    78.7     0
 2 Gunnar Henderson     683002 117.  44.8   -2.82   75.0     0
 3 Elly De La Cruz      682829 114.  19.4   15.4    79.4     0
 4 Jose Ramirez         608070 113.  30.9   32.7    49.7     0
 5 Zach Neto            687263 110.   3.57  15.4    91.2     0
 6 Marcus Semien        543760 108.   0.501 17.7    89.6     0
 7 Ketel Marte          606466 101.  35.2   10.5    55.3     0
 8 Vladimir Guerrero    665489  99.0 47.3   -0.734  52.4     0
 9 Francisco Lindor     596019  98.5 30.6    0.699  67.2     0
10 Jose Altuve          514888  98.2 19.3   13.9    65.0     0

Replacement Level

Recap

  • \(\textrm{RAA} = \textrm{RAA}^{(b)} + \textrm{RAA}^{(br)} + \textrm{RAA}^{(f)} + \textrm{RAA}^{(p)}\)
  • Comprehensive measure of player performance in all parts of the game
  • Absolute \(\textrm{RAA}\) are interesting…
  • … but are much more useful when calibrated to some baseline

Replacement Level

Replacement level is simply the level of production you could get from a player that would cost you nothing but the league minimum salary to acquire.

  • Definition is fairly arbitrary!

we believe that a team making the MLB minimum would win about 29.7% of its games in a give year, or roughly 47-48 per team

Roster-based Definition

  • Most MLB teams carry 12 pitchers & 13 position players
  • On any given day:
    • \(30 \times 12 = 360\) available pitchers
    • \(30 \times 13 = 390\) available position players
  • Sort position players by number of at-bats in which they batted
    • Top 390: not-replacement
  • Sort pitchers by numbers of at-bats in which they pitched
    • Top 360: not-replacement

Identifying Non-Replacement Players

all_players <- unique(
  c(def_atbat2024$batter, def_atbat2024$pitcher, def_atbat2024$fielder_2,
    def_atbat2024$fielder_3, def_atbat2024$fielder_4, def_atbat2024$fielder_5,
    def_atbat2024$fielder_6, def_atbat2024$fielder_7, def_atbat2024$fielder_8, def_atbat2024$fielder_9))
pitchers <- unique(def_atbat2024$pitcher)
position_players <- all_players[!all_players %in% pitchers]
position_pa <-
  def_atbat2024 |>
  dplyr::filter(batter %in% position_players) |>
  dplyr::group_by(batter) |>
  dplyr::summarise(n = dplyr::n()) |>
  dplyr::arrange(dplyr::desc(n)) |>
  dplyr::rename(key_mlbam = batter)

pitcher_pa <-
  def_atbat2024 |>
  dplyr::group_by(pitcher) |>
  dplyr::summarise(n = dplyr::n()) |>
  dplyr::arrange(dplyr::desc(n)) |>
  dplyr::rename(key_mlbam = pitcher)
repl_position_players <- position_pa$key_mlbam[-(1:390)]
repl_pitchers <- pitcher_pa$key_mlbam[-(1:360)]

cat("Cut-off for position players:", position_pa$n[390], "\n")
cat("Cut-off for pitchers:", pitcher_pa$n[360], "\n")
Cut-off for position players: 131 
Cut-off for pitchers: 204

Replacement-Level Per-At-Bat RAA

  • If we replace Ohtani w/ a replacement-level player, what \(\textrm{RAA}\) values would they achieve?
  • Idea: multiply Ohtani’s number of at-bats by average per-at-bat \(\textrm{RAA}\) of replacement-level players
  • Divide total \(\textrm{RAA}\) for all replacement-level players by total number of at-bats
repl_position_raa <-
  raa |>
  dplyr::filter(key_mlbam %in% repl_position_players) |>
  dplyr::inner_join(y = position_pa, by = "key_mlbam") |>
  dplyr::select(Name, key_mlbam, RAA, n)

repl_pitch_raa <-
  raa |>
  dplyr::filter(key_mlbam %in% repl_pitchers) |>
  dplyr::inner_join(y = pitcher_pa, by = "key_mlbam") |>
  dplyr::select(Name, key_mlbam, RAA, n) 

repl_avg_pos <- sum(repl_position_raa$RAA)/sum(repl_position_raa$n)
repl_avg_pitch <- sum(repl_pitch_raa$RAA)/sum(repl_pitch_raa$n)

cat("Replacement-level per-at-bat RAA (position players):", round(repl_avg_pos, digits = 4), "\n")
cat("Replacement-level per-at-bat RAA (pitchers):", round(repl_avg_pitch, digits = 4),"\n")
Replacement-level per-at-bat RAA (position players): -0.002 
Replacement-level per-at-bat RAA (pitchers): -0.0243

Position Player WAR

  • Compare player’s RAA to what replacement-level would achieve in same opportunities
  • 1 Win = 10 Runs
position_war <-
  raa |>
  dplyr::filter(!key_mlbam %in% repl_position_players) |>
  dplyr::inner_join(y = position_pa, by = "key_mlbam") |> 
  dplyr::select(Name, key_mlbam, RAA, n) |>
  dplyr::mutate(shadowRAA = n * repl_avg_pos) |>
  dplyr::mutate(WAR = (RAA - shadowRAA)/10)
# A tibble: 10 × 6
   Name              key_mlbam   RAA     n shadowRAA   WAR
   <chr>                 <dbl> <dbl> <int>     <dbl> <dbl>
 1 Bobby Witt           677951 165.    694     -1.36 16.6 
 2 Gunnar Henderson     683002 117.    702     -1.37 11.8 
 3 Elly De La Cruz      682829 114.    679     -1.33 11.5 
 4 Jose Ramirez         608070 113.    657     -1.28 11.5 
 5 Zach Neto            687263 110.    590     -1.15 11.1 
 6 Marcus Semien        543760 108.    701     -1.37 10.9 
 7 Ketel Marte          606466 101.    562     -1.10 10.2 
 8 Vladimir Guerrero    665489  99.0   671     -1.31 10.0 
 9 Francisco Lindor     596019  98.5   689     -1.35  9.98
10 Jose Altuve          514888  98.2   661     -1.29  9.95

Looking Ahead

  • Tonight: Guest lecture by Namita Nanadakumar (Seattle Kraken)
    • 6:00pm in Morgridge Hall 1524
    • Sponsored by Sports Analytics Club
  • Adjusted Office Hours:
    • Today: 4pm - 5:30pm in MH 5586
    • Wednesday: 4pm - 5pm in MH 5586 (not 3pm!)
  • Before Lecture 9: please read Chapters 7 & 8 of Beyond Multiple Linear Regression