STAT479 Lecture 25

Next Steps

Additional Topics

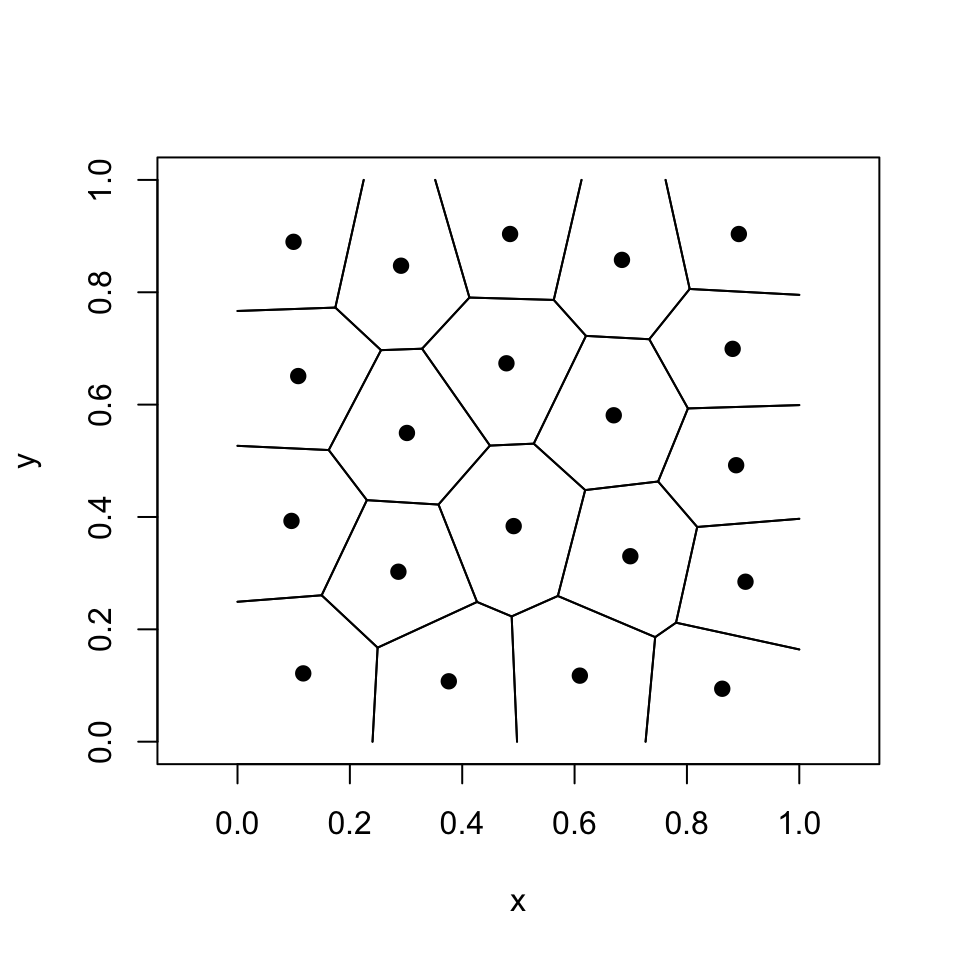
Voronoi Tesselations (definition)

Consider \(n\) points \(x_{1}, \ldots x_{n}\) in space \(\mathbb{X}\)
Let \(d(\cdot, \cdot)\) be distance metric on \(\mathbb{X}\)
For each \(i = 1, \ldots, n\) define \(\mathcal{X}_{i}\) as \[ \mathcal{X}_{i} = \left\{x \in \mathbb{X}: d(x, x_{i}) \leq d(x, x_{j}) \text{ for all } j \neq i\right\} \]
\(\mathcal{X}_{i}\): all points in \(\mathbb{X}\) closer to \(x_{i}\) than to any other \(x_{j}\)

Voroni Tesselation (example)

Can compute using deldir package in R

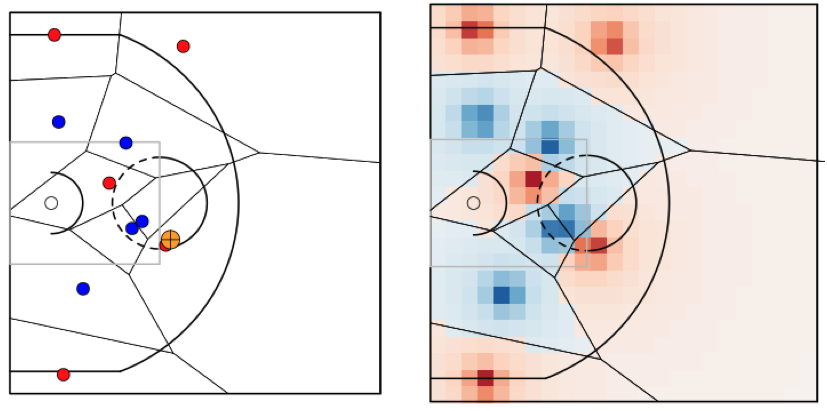
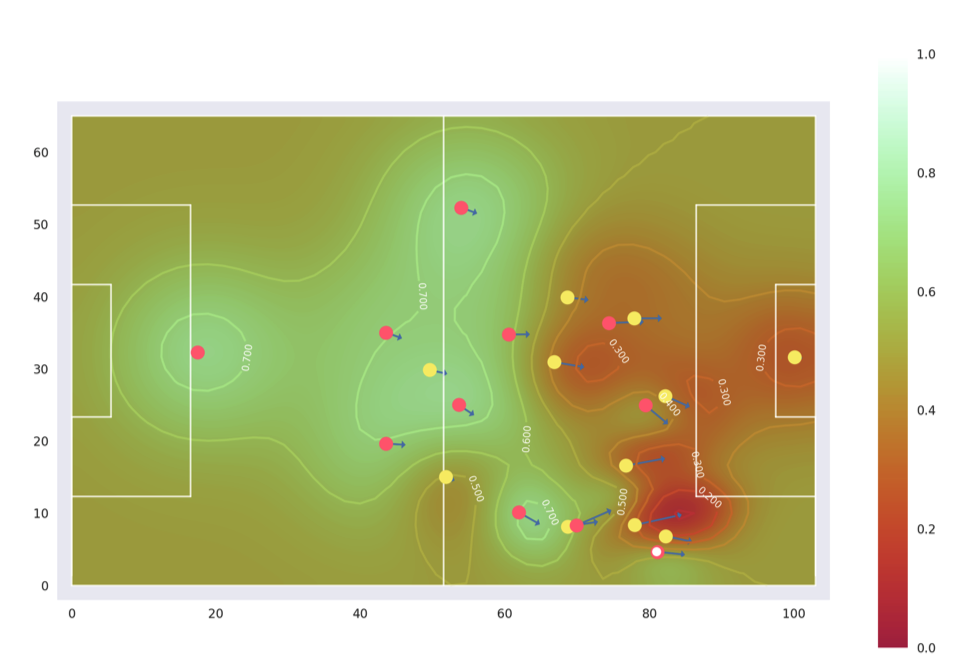
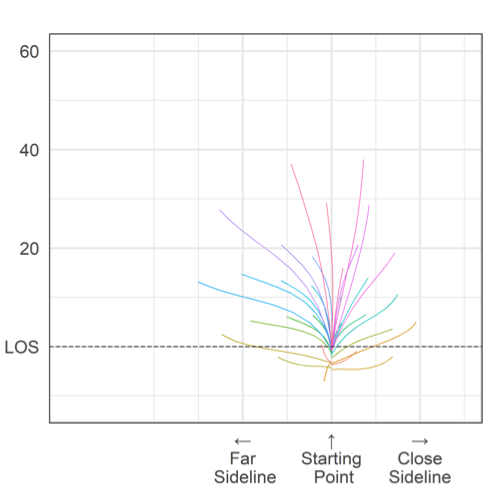
Voronoi Tesselations (applications)

Cervone et al. (2016): definition of court ownership
Quantify impact of different actions in terms of how much space/court value was created

Continuous Space Ownership

Fernandez & Bornn (2018): incorporated speed & direction
Facilitates continuous understanding of space ownershp

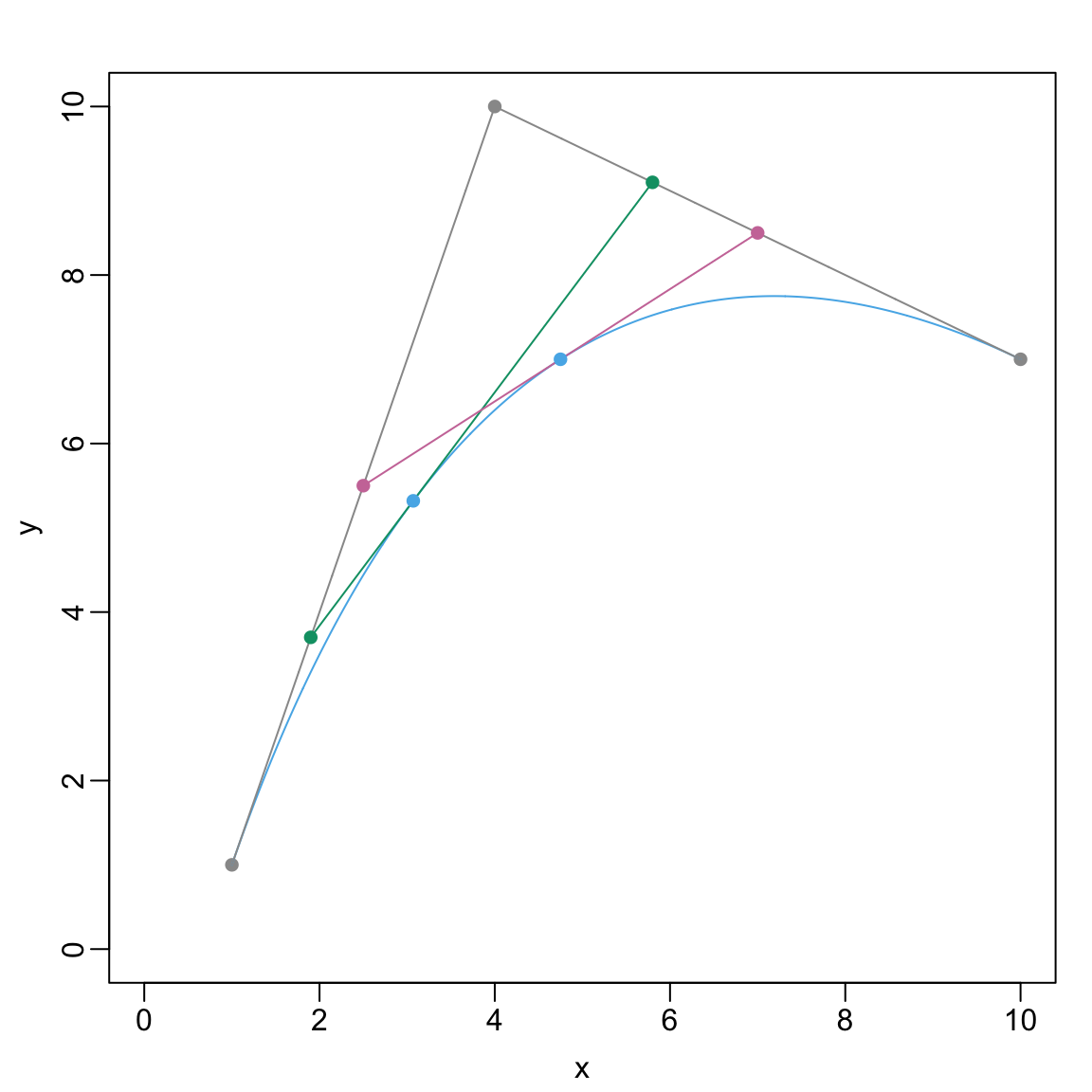
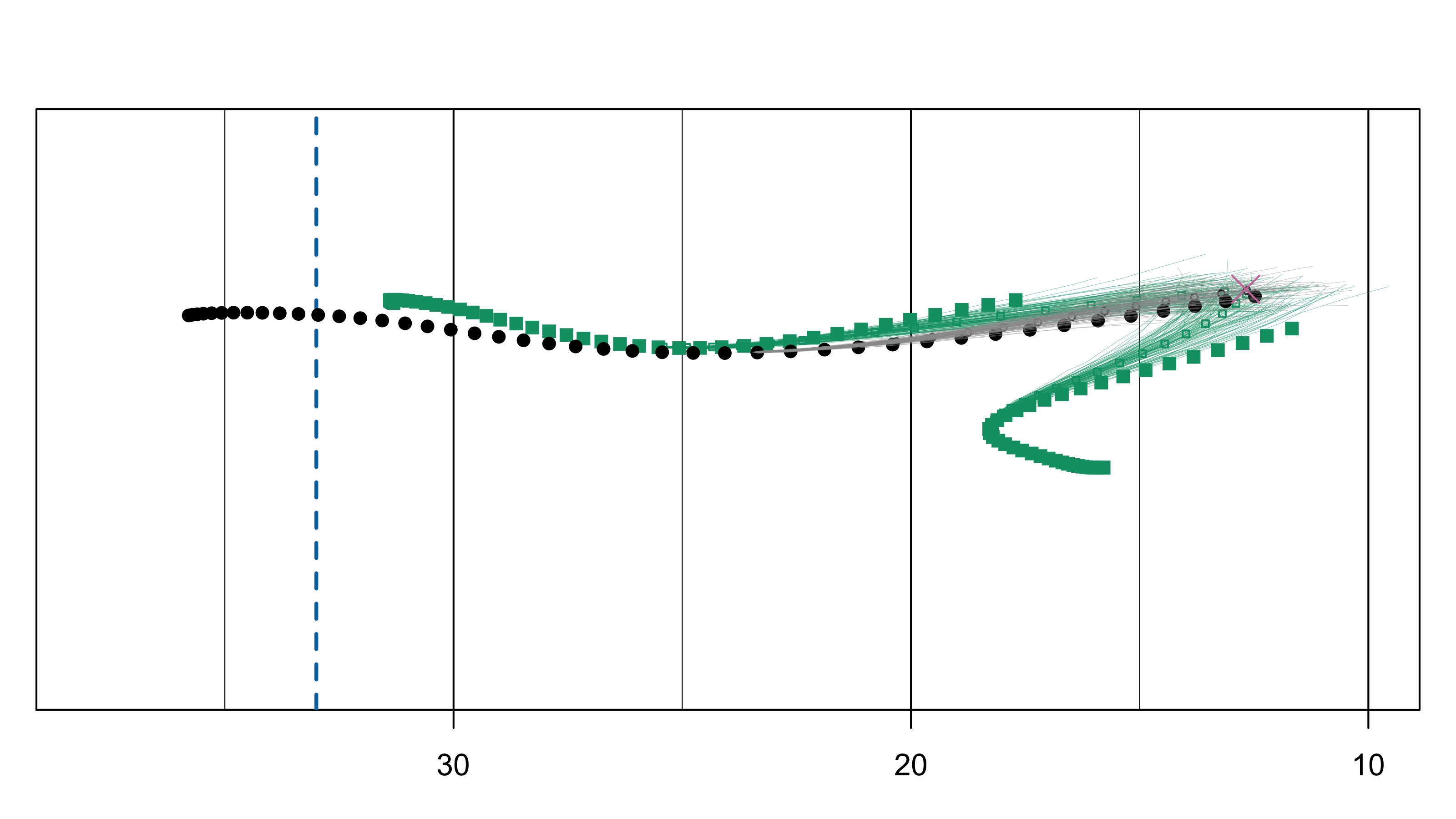
Bezier Curves (definition)

Given \(D+1\) control points \(\boldsymbol{b}_{0}, \ldots, \boldsymbol{b}_{D}\) in \(\mathbb{R}^{2}\)
Degree \(D\) Bezier curve is \[ \boldsymbol{x}(t) = \sum_{d = 0}^{D}{\binom{D}{d}t^{d}(1-t)^{D-d}\boldsymbol{b}_{d}}. \]
\(\boldsymbol{x}(0) = \boldsymbol{b}_{0}\) and \(\boldsymbol{x}(1) = \boldsymbol{b}_{D}\)
Used widely in computer graphics

Bezier Curve Example 1

Figure 1: Quadratic Bezier curve example

Bezier Curve Example 2

Figure 2: Quadratic Bezier curve example

Bezier Curve Applications I

Miller & Bornn (2017): clusters of NBA actions

Bezier Curve Applications II

Chu et al. (2019): clustering NFL routes

Bezier Curve Applications III

Bayesian model: prior over control points \(\Rightarrow\) posterior over remaining trajectory

Next Steps

Additional Training

Calculus-based probability: STAT/MATH 309, STAT 409, or MATH 431
- Understanding joint, conditional, and marginal probabilities
- Common distributions are building blocks of more sophisticated models
Statistical inference: STAT/MATH 310, STAT 410
Bayesian Statistics: STAT 479 (Fall 2027)
- Bayes Rules!: Very good (online) textbook
- Email me if you’d like to sit in on STAT 775 next semester (MW 9:30-10:45)
Fundamental: gain experience w/ modeling

Building Your Portfolio

Continue developing your projects!
- Build more sophisticated models
- Run more elaborate calculations/simulation
- Re-assess certain analysis decisions
Work on personal research projects
Focus on answering substantive questions
Essential: put your code on GitHub

Thanks!

Super appreciate y’all’s enthusiasm, effort, & patience
Stay in touch!